І. Опрацюйте теоретичний матеріал:
Теорема: Кожна сторона трикутника менша від суми двох інших його сторін.
Доведення
Розглянемо довільний трикутник АОС і покажемо, що АВ < ВС + СА
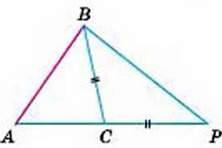
Для доведення відкладемо на продовженні сторони АС відрізок СР, що дорівнює стороні ВС, і розглянемо трикутник АВР. Кути СВР і СРВ – рівні, бо СВ = СР. Кут АВР – більший за ∠P.
А оскільки проти більшого кута лежить більша сторона, то АВ < АР. Врахувавши, що АР = АС + СР = АС + СВ, маємо: АВ < АС + СВ.
Так само можна показати, що ВС < СА + АВ, АС < СВ + ВА.
З доведеної теореми випливає таке твердження:
Якщо точки А, В, С не лежать на одній прямій, то правильні нерівності:
АВ < ВС + СА,
ВС < СА + АВ,
АС < СВ + ВА.
Кожну з цих трьох нерівностей називають нерівністю трикутника.
Наслідок з теореми: Кожна зі сторін трикутника більша за різницю двох інших його сторін.
З теореми про нерівність трикутника та наслідку з неї отримаємо важливе співвідношення між сторонами трикутника: кожна сторона трикутника менша від суми двох інших сторін, але більша за модуль їх різниці.

ІІ. Опрацюйте навчальне відео (розглянуті завдання запишіть в зошит як класну роботу):
У відео розв’язуються наступні задачі:
Завдання 1. Дві сторони трикутника дорівнюють 2,9см і 8,3см. Якому найбільшому цілому числу см може дорівнювати третя сторона трикутника.
Завдання 2. Дві сторони трикутника дорівнюють 2,9см і 4,5см. Якому найменшому цілому числу см може дорівнювати третя сторона трикутника
Завдання 3. Дві сторони рівнобедреного трикутника дорівнюють 5см і 11см. Знайдіть периметр даного трикутника
