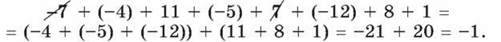І. Опрацюйте теоретичний матеріал (розглянуті приклади запишіть в зошит як класну роботу):
Для додавання раціональних чисел, як і для додавання додатних чисел, справджуються переставна і сполучна властивості.
Переставна властивість додавання.
Для будь-яких раціональних чисел а і b виконується рівність а + b = b + а.
Перевіримо цю властивість на прикладах.
Приклад 1. -8 + (-3) = -11; -3 + (-8) = -11, тому -8 + (-3) = -3 + (-8).
Приклад 2. -2 + 5 = 3; 5 + (-2) = 3, тому -2 + 5 = 5 + (-2).
Сполучна властивість додавання.
Для будь-яких раціональних чисел а, b і c виконується рівність (а+ b) + c = а + (b + c).
Перевіримо цю властивість на прикладі.
Приклад 3. (-2 + 7) + (-8) = 5 + (-8) = -3; -2 + (7 + (-8)) = -2 + (-1) = -3, тому (-2 + 7) + (-8) = -2 + (7 + (-8)).
Для будь-якого раціонального числа а виконуються рівності:
а + 0 = 0 + а = а;
а + (-а) = – а + а =0.
Властивості додавання дають можливість спростити процес обчислення суми кількох доданків, обираючи зручний порядок обчислень. Якщо необхідно додати кілька чисел, серед яких є додатні і від’ємні числа, то можна окремо додати всі додатні числа і окремо всі від’ємні, а потім до суми додатних чисел додати суму від’ємних. Якщо серед доданків є протилежні числа, то сума цих доданків дорівнює нулю. Такі доданки можна закреслити (кажуть, що доданки взаємно знищилися).
Приклад 4. Обчислити суму: -7 + (-4) + 11 + (-5) + 7 + (-12) + 8 + 1.
Розв’язання. Зазначимо, що серед доданків є протилежні числа: -7 і 7, сума яких дорівнює нулю. Їх можна закреслити. Далі згрупуємо числа з однаковими знаками: